被dp折磨了许久后整理的博客 DP(动态规划,dynamic programming)
多阶段决策过程的最优解 将一个问题分解成多个互相关联的阶段,每个阶段都要做出最优的决策,从而使整个过程达到最好的活动效果。每个阶段决策的选取既依赖于当前的状态,有影响以后的发展。
动态规划的最优化原理 无论过去的状态和决策如何,对前面的决策所形成的状态而言,余下的诸决定必须构成最优策略的性质。也可以通俗的理解为子问题地局部最优将导致问题的全局最优,即问题具有最优子结构的性质,也就是说一个问题的最优解只取决于其子问题的最优解,而非最优解对问题的求解没有影响。
动态规划的无后效性 指的是某阶段的性质一旦确定,则此后过程的演变不再受此前各状态及决策的影响。也就是说,“未来与过去无关”,当前的状态是历史状态的总结,此前的历史只能通过当前状态去影响过去未来的演变。
然后基本思路就有辣!
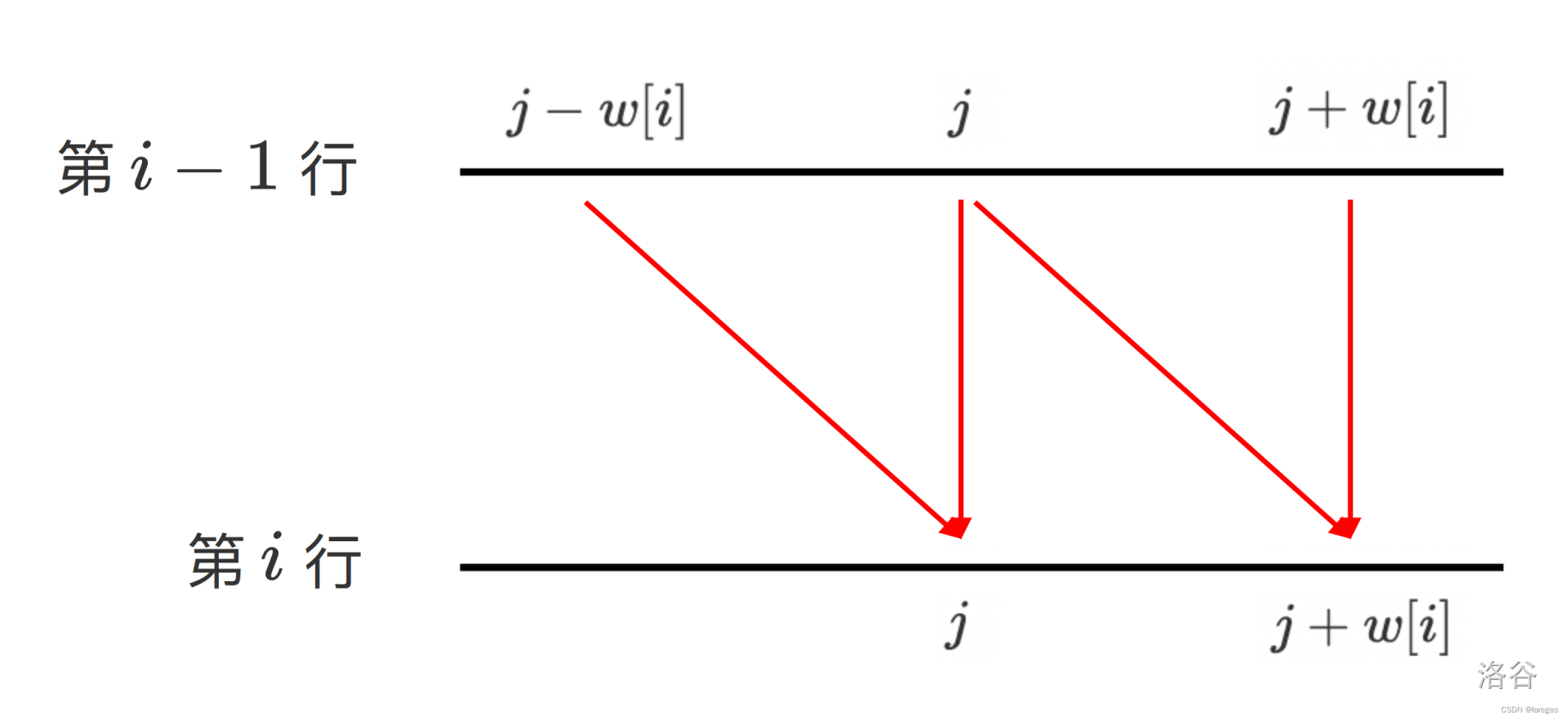
dp常用模型 背包 01背包 dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[i]]+v[i])
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <bits/stdc++.h> using namespace std;int t,n;const int maxn = 1010 ;int w[maxn],val[maxn];int dp[maxn][maxn];int main () cin >> n >> t; for (int i = 1 ; i <= n; i++) { cin >> w[i] >> val[i]; } for (int i = 1 ; i <= n; i++) for (int j = t;j >= 0 ;j--) { if (j >= w[i]) { dp[i][j] = max (dp[i-1 ][j-w[i]]+val[i],dp[i-1 ][j]); } else { dp[i][j] = dp[i-1 ][j]; } } int res = 0 ; for (int i = 1 ; i <= n; i++) res = max (res,dp[i][t]); cout << res; return 0 ; }
可以看出只需要简单的递推便可以做出二维dp
完全不能看得出来可以继续优化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;int t,n;const int maxn = 1010 ;int w[maxn],val[maxn];int dp[maxn];int main () cin >> n >> t; for (int i = 1 ; i <= n; i++) { cin >> w[i] >> val[i]; } for (int i = 1 ; i <= n ;i++) for (int j = t; j >= w[i]; j--) { dp[j] = max (dp[j],dp[j-w[i]]+val[i]); } cout << dp[t]; return 0 ; }
令人十分甚至九分高兴的一维dp便事了
完全背包
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 #include <bits/stdc++.h> using namespace std;const int N = 10010 ;int n, m;int f[N];int v[N], w[N];int main () ios::sync_with_stdio (0 ), cin.tie (0 ), cout.tie (0 ); cin >> n >> m; for (int i = 1 ; i <= n; i ++){ cin >> v[i] >> w[i]; } for (int i = 1 ; i <= n ; i ++) for (int j = v[i]; j <= m; j ++) f[j] = max (f[j], f[j - v[i]] + w[i]); cout << f[m]; return 0 ;
区别在于,这一次j是从小到大遍历的,如果在01背包中这么做,那么会导致上一层数据被覆盖,结果出错。dp[i][j] = max(dp[i−1][j],dp[i][j−w[i]]+v[i]) (此处先将k省去)可以看出除非一件不取,否则都是根据本层的数据进行规划,刚好符合j递增形成的递推。其实有点懒就没有打二维未优化版本了
关于j的遍历顺序再讨论 实在没想到,即使很不想还是得再对这个问题讨论(下列讨论大部分都是在进行一维数组优化时考虑的)。
那么继续多重背包level1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <bits/stdc++.h> using namespace std;const int N = 110 ;int n,m;int f[N];int main () cin >> n >> m; for (int i = 1 ; i <= n; i++) { int v,w,s; cin >> v >> w >> s; for (int j = m; j>= 0 ; j--) for (int k = 1 ; k <= s && k*v <= j; k ++) f[j] = max (f[j],f[j-k*v]+k*w); } cout <<f[m]; return 0 ; }
与完全背包同理,只不过加一个循环来限制拿的个数。到此为止都是很正常的。等一下就不一定了多重背包level2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <bits/stdc++.h> using namespace std;const int N = 11010 , M = 2010 ;int w[N], v[N];int dp[M];int main () ios::sync_with_stdio (false ); cin.tie (nullptr ); int n, m; cin >> n >> m; int cnt = 0 ; while (n--) { int a, b, s; cin >> a >> b >> s; for (int k = 1 ; k <= s; k *= 2 ) { cnt++; w[cnt] = a * k, v[cnt] = b * k; s -= k; } if (s > 0 ) { cnt++; w[cnt] = a * s, v[cnt] = b * s; } } n = cnt; for (int i = 1 ; i <= n; i++) for (int j = m; j >= w[i]; j--) dp[j] = max (dp[j], dp[j - w[i]] + v[i]);。 cout << dp[m] << "\n" ; return 0 ; }
在这里使用了二进制优化
二进制优化 在这里先举个例子,比如说一个物品可以拿7个,那么正常情况下便如同01背包,将它分解为7件价值与质量一致的物品便可以了。但是显然这样的时间复杂度太高了,所以说我们可以找到对应7的1,2,4三个数。
多重背包level3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <bits/stdc++.h> using namespace std;const int N = 20010 ;int n, m;int f[N], g[N], q[N];int main () cin >> n >> m; for (int i = 0 ; i < n; i++) { int c, w, s; cin >> c >> w >> s; memcpy (g,f,sizeof (f)); for (int j = 0 ; j < c; j ++) { int hh = 0 , tt = -1 ; for (int k = j; k <= m; k += c) { f[k] = g[k]; if (hh <= tt && k - s*c > q[hh]) hh ++; if (hh <= tt ) f[k] = max (f[k],g[q[hh]]+(k - q[hh])/ c * w); while (hh <= tt && g[q[tt]] - (q[tt] - j) / c * w <= g[k] - (k-j) / c*w) tt--; q[++tt] = k; } } } cout << f[m] << endl; }
由于其高要求 离谱
单调队列优化 滑雪
[SHOI2002] 滑雪 题目描述 Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5 1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 $24-17-16-1$(从 $24$ 开始,在 $1$ 结束)。当然 $25$-$24$-$23$-$\ldots$-$3$-$2$-$1$ 更长。事实上,这是最长的一条。
输入格式 输入的第一行为表示区域的二维数组的行数 $R$ 和列数 $C$。下面是 $R$ 行,每行有 $C$ 个数,代表高度(两个数字之间用 $1$ 个空格间隔)。
输出格式 输出区域中最长滑坡的长度。
样例 #1 样例输入 #1 1 2 3 4 5 6 5 5 1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9
样例输出 #1 提示 对于 $100%$ 的数据,$1\leq R,C\leq 100$。
一眼得出递推式 f[x][y] = max(f[x-1][y],f[x+1][y],f[x][y+1],f[x][y-1]) 寄吧从哪里开始计算呢?
这时候优先队列便是个好东西了(以下是洛谷题解区大佬代码)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <iostream> #include <queue> using namespace std;struct node { int i,j,num,f; }; struct cmp1 { bool operator () (node x,node y) return x.num>y.num; } }; priority_queue<node,vector<node>,cmp1>q; int n,m,maxn,maxj,maxi,w,top=0 ,g[101 ][101 ],f[101 ][101 ];int main () cin>>n>>m; for (int i=1 ;i<=n;i++){ for (int j=1 ;j<=m;j++){ f[i][j]=1 ; cin>>g[i][j]; node a; a.i=i;a.j=j;a.f=0 ;a.num=g[i][j]; q.push (a); } } while (!q.empty ()){ node now1=q.top (); int i=now1.i; int j=now1.j; int now=now1.num; q.pop (); if (g[i-1 ][j]<now) f[i][j]=max (f[i][j],f[i-1 ][j]+1 ); if (g[i+1 ][j]<now) f[i][j]=max (f[i][j],f[i+1 ][j]+1 ); if (g[i][j-1 ]<now) f[i][j]=max (f[i][j],f[i][j-1 ]+1 ); if (g[i][j+1 ]<now) f[i][j]=max (f[i][j],f[i][j+1 ]+1 ); if (maxn<f[i][j]) maxn=f[i][j]; } cout<<maxn; return 0 ; }
我的理解是开了储存有高度,位置,以及num(优先度)的 结构体 后优先队列 。然后再从高到低开始判断,此处便如同完全背包中j必须从大到小遍历同样的原理,否则会覆盖比自己高度还要高的位置的数据,但滑雪确实不可能从低处滑向高处的。所以必须 从高向低 进行df。